ŞIRURI t-DERIVABILE

de Maria Bătineţu-Giurgiu, D. M. Bătineţu-Giurgiu şi Mihály Bencze

În memoria profesorului Ilie Iliescu

În [3] am introdus conceptul de şir derivabil, prezentând totodată unele proprietăţi şi aplicaţii ale acestui concept. Mai departe, ne propunem să extindem acest concept introducând definiţia şirurilor t-derivabile, unde .

Fie un şir convergent de numere reale. Pentru orice vom nota:

. (1)

Definiţia 1. Fie un şir convergent de numere reale şi . Dacă există:

, (2)

vom spune că şirul admite o t-derivată. Dacă şirul admite o t-derivată , atunci spunem că şirul este un şir t-derivabil.

Definiţia 2. Dacă şirul de numere reale este un şir pentru care , vom spune că şirul admite o a doua t-derivată, dacă există:

. (3)

Dacă , atunci spunem că şirul este un şir de două ori t-derivabil. Prin urmare putem defini, din aproape în aproape, t-derivata , , a şirului şi anume:

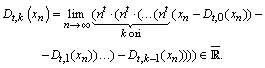(4)

Dacă , , … , , atunci spunem că şirul este t-derivabil de k ori, . Dacă şirul este t-derivabil de k ori, pentru orice , spunem că acest şir este indefinit t-derivabil. În acest caz avem:

, (5)

adică are loc t-dezvoltarea (t-expresia) asimptotică a şirului .

Observaţie. Orice şir convergent este t-derivabil dacă .

Într-adevăr, dacă , atunci:

.

Dacă , atunci avem:

.

De aceea vom considera în continuare .

Dacă un şir 1-derivabil se va numi, conform cu [3], un şir derivabil.

Propoziţia 1. Oricare ar fi , există cel puţin un şir t-derivabil.

Demonstraţie. Fie şirul , ; atunci acest şir este t-derivabil.

Într-adevăr, avem , şi atunci:

, .

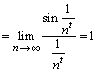Propoziţia 2. Dacă şirul este t-derivabil, atunci:

.

Demonstraţie. Avem:

.

După cum am arătat în [3] reciproca acestei propoziţii nu este adevărată.

1. Câteva exemple de şiruri t-derivabile şi şiruri t-nederivabile

1.1. Şirul , nu admite o t-derivată. Într-adevăr:

, dar:

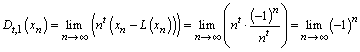nu există. Deci şirul nu admite o t-derivată.

1.2. Fie şirul , şirul lui Andrei G. Ioachimescu, de termen general . În [2], problema 2.66, se arată că există (constanta lui Ioachimescu) iar în problema 2.158 din [2] se arată că , adică şirul este derivabil. Prin urmare:

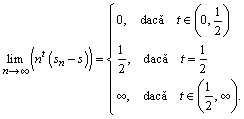
Cu această ocazie demonstrăm:

Propoziţia 3. Dacă este un şir t-derivabil cu , atunci oricare ar fi avem:

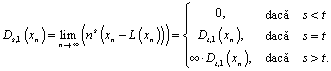
Demonstraţie. Avem:

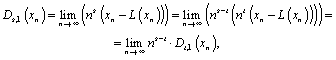
de unde se constată că dacă ; dacă şi dacă . Cu aceasta propoziţia este demonstrată.

După cum am arătat în [3], şirul este derivabil şi (vezi problema 3639 din G.M. vol. XXXIII (1927-1928), pag. 280, problemă propusă de D.V. Ionescu).

De asemenea, în [3] am arătat că şirul lui Lalescu ,

este derivabil şi . Totodată în [3] am arătat că şirul constantei lui Euler este derivabil cu , precum şi şirul lui Ghermănescu ,

este derivabil şi .

Propoziţia 4. Fie f : o funcţie derivabilă pe A, iar un şir t-derivabil cu , şi , . Atunci şirul este t-derivabil, unde .

Demonstraţie. Este evident că:

,

ceea ce demonstrează enunţul.

Propoziţia 5. Fie f : o funcţie derivabilă cu derivata continuă pe. Dacă , sunt şiruri t-derivabile de numere reale cu , , atunci şirul este t-derivabil.

Demonstraţie. Avem relaţia:

. (7)

Pentru fiecare , aplicăm funcţiei f teorema lui Lagrange pe intervalul sau . Deci între x şi x_n există un c_n astfel încât:

. (8)

Deoarece c_n este între x şi x_n, iar , rezultă că . Din relaţia (8) deducem că:

şi atunci relaţia (7) ne conduce la:

.

Propoziţia 6. Fie f : o funcţie continuă pe şi un şir t-derivabil () de numere reale, astfel încât . Atunci:

. (9)

Demonstraţie. Deoarece funcţia f este continuă, atunci ea admite o primitivă F : şi atunci:

,

unde c_n este între x şi x_n, . Prin urmare:

,

unde am ţinut seama că c_n este între x şi x_n, şi atunci implică .

2. Operaţii cu şiruri t-derivabile

Să remarcăm că avem aceleaşi operaţii ca şi la şiruri derivabile precum şi la funcţii derivabile.

2.1. Dacă t, s , este un şir t-derivabil, iar este un şir s-derivabil, atunci:

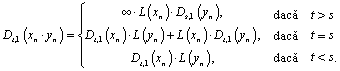(10)

Demonstraţie. Este evident că:

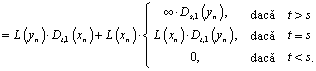(11)

de unde rezultă relaţia din enunţ.

2.2. Dacă şi sunt şiruri de numere reale t-derivabile cu , şi , , atunci şirul este t-derivabil şi:

. (11)

Demonstraţia este aceeaşi ca în [3].

De asemenea, se poate demonstra ca în [3] că dacă este un şir t-derivabil de numere reale strict pozitive, cu , atunci şirul este t-derivabil şi:

. (12)

Urmând pas cu pas operaţiile cu funcţii derivabile se pot demonstra şi alte operaţii cu şiruri t-derivabile (a se vedea [3] şi [4]).

Bibliografie

[1] D. M. Bătineţu, Şiruri, Editura Albatros, Bucureşti, 1979.

[2] D. M. Bătineţu-Giurgiu, Maria Bătineţu-Giurgiu, I. Bârchi-Damian, Augustin Semenescu, Analiză Matematică. Probleme pentru clasa a XI-A, Editura Matrix Rom, Bucureşti, 2003.

[3] Maria Bătineţu-Giurgiu, D. M. Bătineţu-Giurgiu, M. Bencze, Şiruri derivabile, Gazeta Matematică, nr. 9/2005, pag. 410-420.

[4] Maria Bătineţu-Giurgiu, D. M. Bătineţu-Giurgiu, M. Bencze, Derivable sequences, Octogon Mathematical Magazine, vol. 13, nr. 2, october 2005, pag. 936-945.

Profesor univ. dr., Academia Tehnică Militară, Catedra de matematică, Bucureşti

Profesor, C. N. „Matei Basarab“, Bucureşti

Redactor Şef, Revista „Octogon“, Braşov